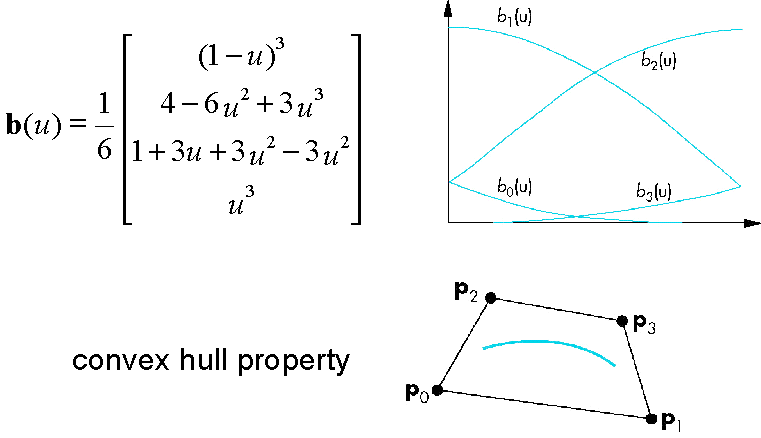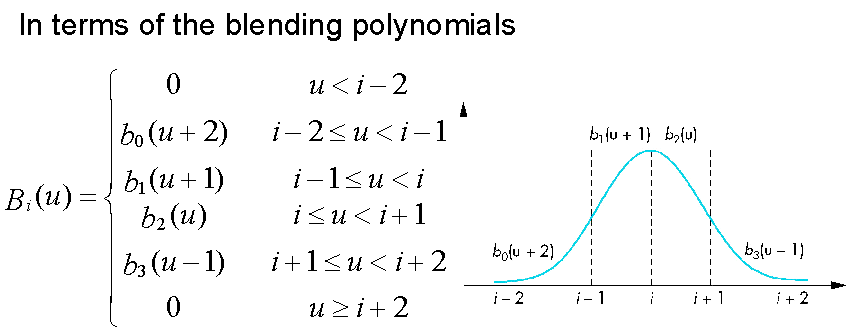CHAPTER 12 - Bezier and Spline Curves, Surfaces

Objectives

Bezier's Idea

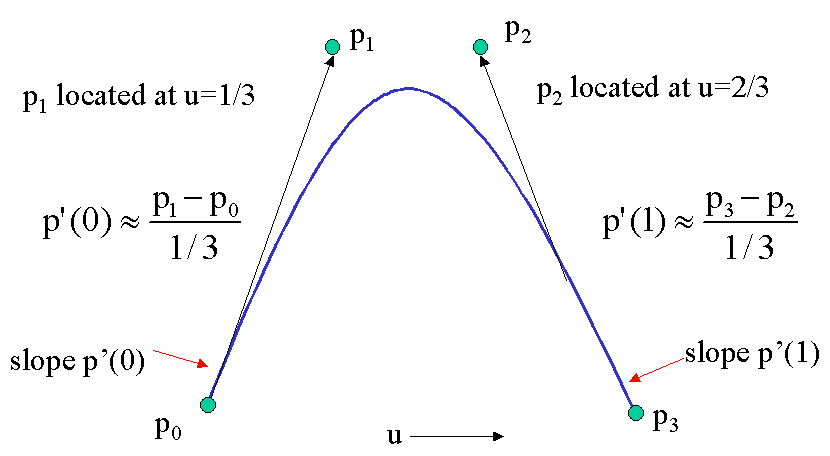
In graphics and CAD, we do not usually have derivative data
Bezier suggested using the same 4 data points as with the cubic interpolating curve to approximate the derivatives in the Hermite form

Approximating Derivatives

Equations

Bezier Matrix

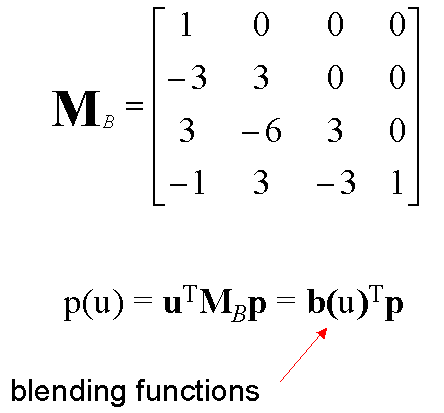
Blending Functions

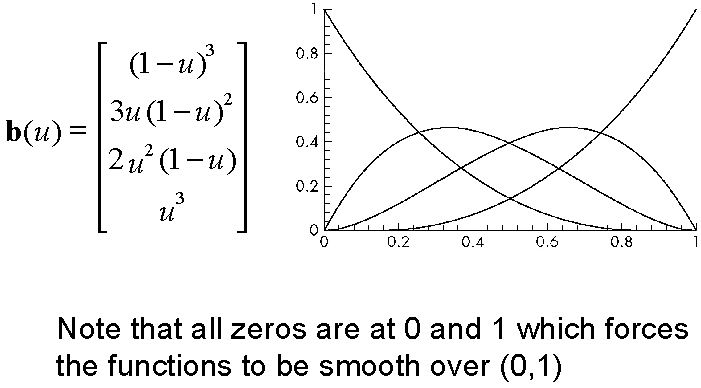
Bernstein Polynomials

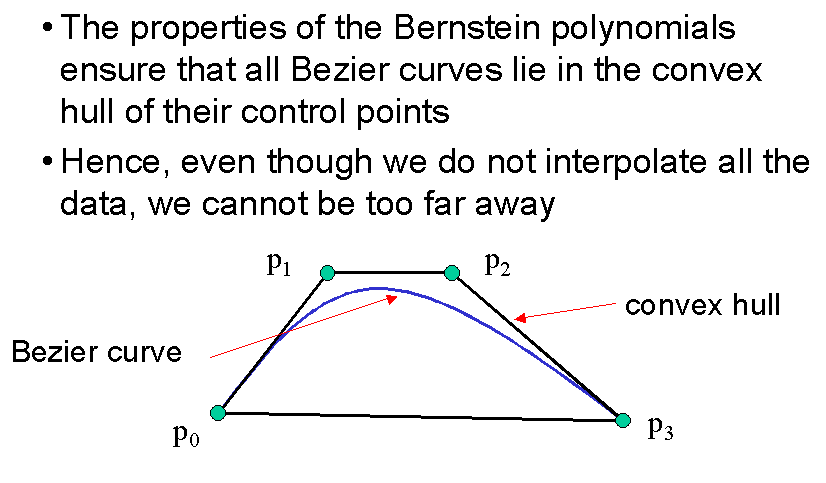
Convex Hull Property

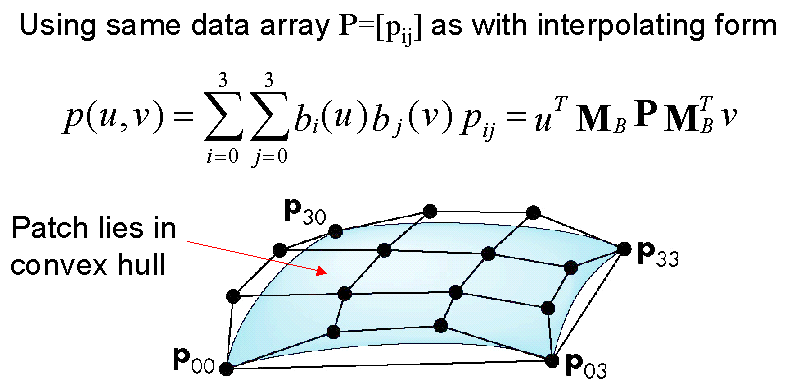
Bezier Patchs

Analysis

Although the Bezier form is much better than the interpolating form, the derivatives are not continuous at join points
Can we do better?
- Go to higher order Bezier
  - More work
  - Derivative continuity still only approximate
  - Supported by OpenGL
- Apply different conditions
  - Tricky without letting order increase

B-Splines

Basis splines: use the data at p=[p_i-2 p_i-1 p_i p_i-1]^T to define curve only between p_i-1 and p_i
Allows us to apply more continuity conditions to each segment
For cubics, we can have continuity of function, first and second derivatives at join points
Cost is 3 times as much work for curves
- Add one new point each time rather than three
For surfaces, we do 9 times as much work

Cubic B-Spline

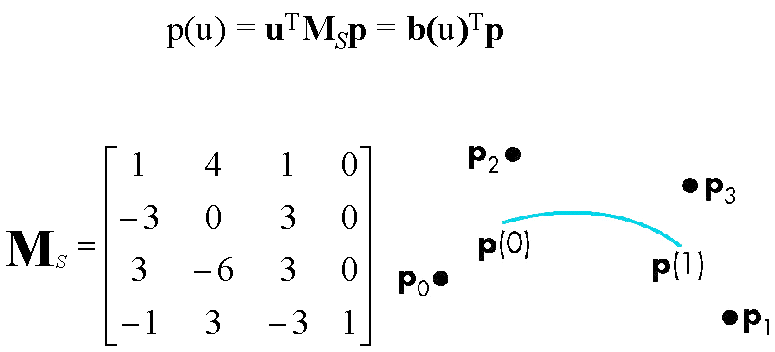
Blending Functions

B-Spline Patches

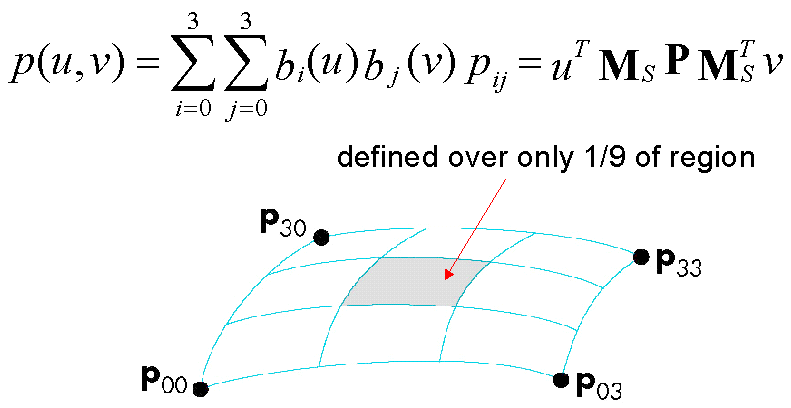
Splines and Basis

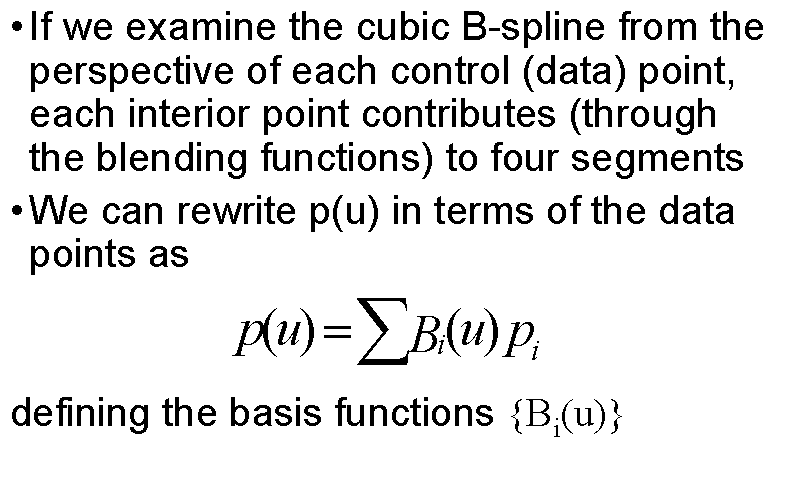
Basis Functions

Generalizing Splines

We can extend to splines of any degree
Data and conditions to not have to be given at equally spaced values (the knots)
- Nonuniform and uniform splines
- Can have repeated knots
  - Can force spline to interpolate points
Cox-deBoor recursion gives method of evaluation

Nurbs

Nonuniform Rational B-Spline curves and surfaces add a fourth variable w to x,y,z
- Can interpret as weight to give more importance to some control data
- Can also interpret as moving to homogeneous coordinate
Requires a perspective division
- NURBS act correctly for perspective viewing
Quadrics are a special case of NURBS