CHAPTER 12 - Parametric Cubic Curves

Objectives

Matrix-Vector Form

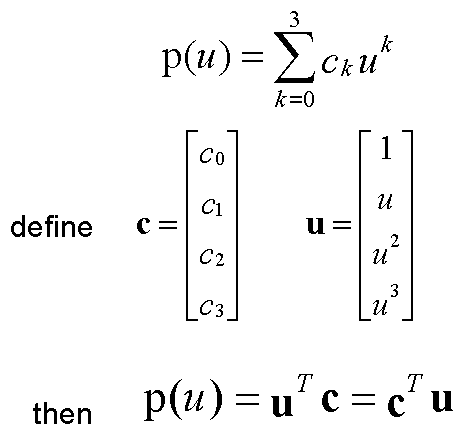
Interpolating Curve

Interpolation Equations

Interpolation Matrix

Interpolating Multiple Segments

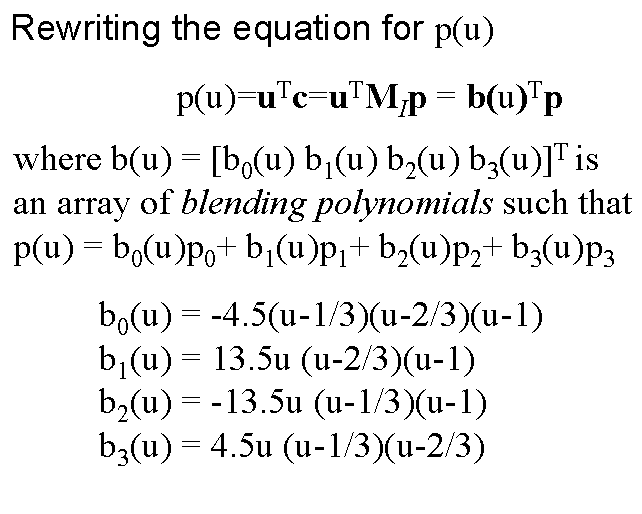
Blending Functions

Interpolating a Patch

Matrix Form

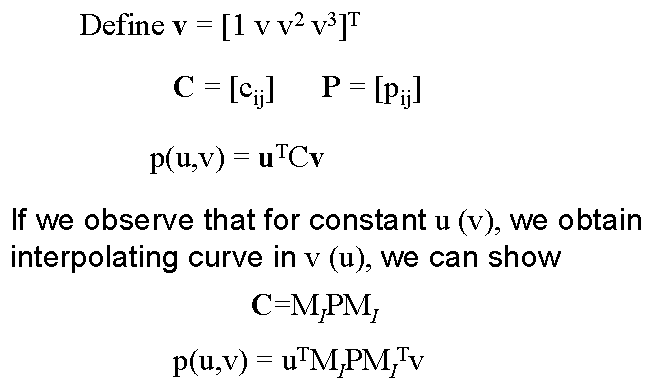
Blending Patches

Other Types of Curves and Surfaces

How can we get around the limitations of the interpolating form
- Lack of smoothness
- Discontinuous derivatives at join points
We have four conditions (for cubics) that we can apply to each segment
- Use them other than for interpolation
- Need only come close to the data

Hermite Form

Equations

Matrix Form

Blending Polynomials

Parametric and Geometric Continuity

We can require the derivatives of x, y,and z to each be continuous at join points (parametric continuity)
Alternately, we can only require that the tangents of the resulting curve be continuous (geometry continuity)
The latter gives more flexibility as we have need satisfy only two conditions rather than three at each join point

Example

Higher Dimensional Approximations

The techniques for both interpolating and Hermite curves can be used with higher dimensional parametric polynomials
For interpolating form, the resulting matrix becomes increasingly more ill-conditioned and the resulting curves less smooth and more prone to numerical errors
In both cases, there is more work in rendering the resulting polynomial curves and surfaces