chapter 4.1

Objectives

Introduce the elements of geometry
- Scalars
- Vectors
- Points
Develop mathematical operations among them in a coordinate-free manner
Define basic primitives
- Line segments
- Polygons

Basic Elements

Geometry is the study of the relationships among objects in an n-dimensional space
- In computer graphics, we are interested in objects that exist in three dimensions
Want a minimum set of primitives from which we can build more sophisticated objects
We will need three basic elements
- Scalars
- Vectors
- Points

Coordinate-Free Geometry

When we learned simple geometry, most of us started with a Cartesian approach
- Points were at locations in space p=(x,y,z)
- We derived results by algebraic manipulations involving these coordinates
This approach was nonphysical
- Physically, points exist regardless of the location of an arbitrary coordinate system
- Most geometric results are independent of the coordinate system
- Euclidean geometry: two triangles are identical if two corresponding sides and the angle between them are identical

Scalars

Need three basic elements in geometry
- Scalars, Vectors, Points
Scalars can be defined as members of sets which can be combined by two operations (addition and multiplication) obeying some fundamental axioms (associativity, commutivity, inverses)
Examples include the real and complex number systems under the ordinary rules with which we are familiar
Scalars alone have no geometric properties

Vectors

Physical definition: a vector is a quantity with two attributes
- Direction
- Magnitude
Examples include
- Force
- Velocity
- Directed line segments

Vector Operations

Every vector has an inverse
- Same magnitude but points in opposite direction
Every vector can be multiplied by a scalar
There is a zero vector
- Zero magnitude, undefined orientation
The sum of any two vectors is a vector
- Use head-to-tail axiom

Vector Spaces

and Linear Vector Spaces

Mathematical system for manipulating vectors
Operations
- Scalar-vector multiplication u = av
- Vector-vector addition: v = u + w
Expressions such as
- v = u + 2w - 3r
- make sense in a vector space

Vectors Lack Position

These vectors are identical
- Same direction and magnitude

Vector spaces insufficient for geometry
- Need points

Points

Location in space
Operations allowed between points and vectors
- Point-point subtraction yields a vector
- Equivalent to point-vector addition

Affine Spaces

Point + a vector space
Operations
- Vector-vector addition
- Scalar-vector multiplication
- Point-vector addition
- Scalar-scalar operations
For any point define
- 1 * P = P
- 0 * P = 0 (zero vector)

Lines

Consider all points of the form
- P(a)=P₀ + a(d)
- Set of all points that pass through P₀ in the direction of the vector d

Parametric Form

This form is known as the parametric form of the line
- More robust and general than other forms
- Extends to curves and surfaces
Two-dimensional forms

Explicit: y = mx + h
Implicit: ax + by + c =0
Parametric (a in [0,1]):
- x(a) = (1-a)x₀ + ax₁
- y(a) = (1-a)y₀ + ay₁

Rays and Line Segments

If a >= 0, then P(a) is the ray leaving P₀ in the direction d (as shown above)
If we use two points to define v, then

P(a) = Q + a(R - Q) = Q + av = (1 - a)Q + aR
For 0<=a<=1 we get all the points on the line segment joining R and Q

Convexity

An object is convex iff for any two points in the object all points on the line segment between these points are also in the object

Affine Sums

Consider the sum (affine addition with points Pi and scalars ai - simple extension of adding 2 points as in ray discussion above)
- P = a₁P₁+ a₂P₂+ ... + a_nP_n
- Can show by induction that this sum makes sense iff
  - a₁+ a₂+ ... a_n= 1
  - in which case we have the affine sum of the points P₁, P₂, & .. P_n
  - If, in addition, a_i>=0, we have the convex hull of P₁, P₂, & .. P_n

Convex Hull

Smallest convex object containing P₁, P₂, ..., P_n
Formed by shrink wrapping points

Curves and Surfaces

Curves are one parameter entities of the form P(a) where the function is nonlinear
Surfaces are formed from two-parameter functions P(a, b)
- Linear functions give planes and polygons

Planes

A plane can be determined by a point and two vectors or by three non-collinear points

Triangles

Normals

Every plane has a vector, referred to as n, that is normal (perpendicular, orthogonal) to it
From point-two vector form P(a,b)=R+au+bv, we know we can use the cross product to find n = u x v and the equivalent form
of the plane as (P0 - P) x n = 0, where P0 and P are points on the plane.

Representation

Objectives

Introduce concepts such as dimension and basis
Introduce coordinate systems for representing vectors spaces and frames for representing affine spaces
Discuss change of frames and bases
Introduce homogeneous coordinates

Linear Independence

A set of vectors v1, v2, ..., vn is linearly independent if
- a₁v₁+a₂v₂+... a_nv_n=0 iff a₁= a₂= ...a_n = 0
If a set of vectors is linearly independent, we cannot represent one in terms of the others through any linear combination (scalar multiplication with vector addition) of the vectors
If a set of vectors is linearly dependent, as least one can be written in terms of the others through a linear combination

Dimension

In a linear vector space, the maximum number of linearly independent vectors is fixed and is called the dimension of the space
In an n-dimensional space, any set of n linearly independent vectors form a basis for the space
Given a basis v₁, v₂, ..., v_n, any vector v can be written as a linear combination of the basis vectors

v=a₁v₁+ a₂v₂ + ...+a_nv_n

where the {a_i} are unique

Representation

Until now we have been able to work with geometric entities without using any frame of reference, such as a coordinate system
Need a frame of reference to relate points and objects to our physical world.
- For example, where is a point? Can't answer without a reference system
- World coordinates
- Camera coordinates

Coordinate Systems

Consider a basis v₁, v₂, ..., v_n
A vector is written v=a₁v₁+ a₂v₂ + ... +a_nv_n
The list of scalars {a₁, a₂, ..., a_n} is the representation of v with respect to the given basis
We can write the representation as a row or column matrix of scalars

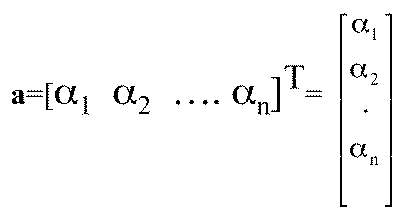
Example

v=2v₁+3v₂-4v₃
a=[2, 3, -4]^T
Note that this representation is with respect to a particular basis
For example, in OpenGL we start by representing vectors using the world basis but later the system needs a representation in terms of the camera or eye basis

Coordinate Systems

Which is correct?

Both are because vectors have no fixed location

Frames

A coordinate system is insufficient to represent points
If we work in an affine space we can add a single point, the origin, to the basis vectors to form a frame

Representation in a Frame

A frame in 3D space is determined by (P₀, v₁, v₂ v₃)
Within this frame, every vector can be written as
- v=a₁v₁+ a₂v₂ + ... +a_nv_n
Every point can be written as
- P = P₀ + b₁v₁+ b₂v₂ + ...+ b_nv_n

Confusing Points and Vectors

Consider the point and the vector

P = P₀ + b₁v₁ + b₂v₂ + ... +b_nv_n

v=a₁v₁+ a₂v₂ + ...+ a_nv_n
They appear to have similar representations

p=[b₁ b₂ b₃] v=[a₁ a₂ a₃]

which confuses the point with the vector
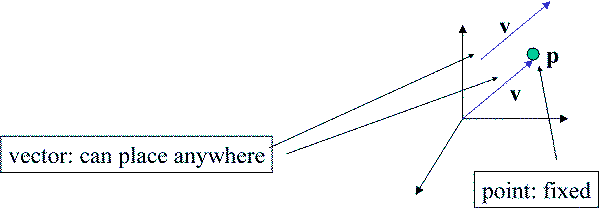
- A vector has no position

A Single Representation

If we define 0 *P = 0 and 1 *P =P then we can write
v=a₁v₁+ a₂v₂ +a₃v₃ = [a₁ a₂ a₃ 0 ] [v₁ v₂ v₃ P₀] ^T
P = P₀ + b₁v₁+ b₂v₂ +b₃v₃= [b₁ b₂ b₃ 1 ] [v₁ v₂ v₃ P₀] ^T

Thus we obtain the four-dimensional homogeneous coordinate representation
v = [a₁ a₂ a₃ 0 ] ^T
p = [b₁ b₂ b₃ 1 ] ^T

Homogeneous Coordinates

The general form of four dimensional homogeneous coordinates for points is
p=[x y z w] ^T
We return to a three dimensional point (for w! = 0) by
x x/w
y y/w
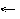z z/w
If w = 0, the representation is that of a vector.
Note that homogeneous coordinates replace points in three dimensions by lines through the origin in four dimensions.

Homogeneous Coordinates and Computer Graphics

Homogeneous coordinates are key to all computer graphics systems
- All standard transformations (rotation, translation, scaling) can be implemented by matrix multiplications with 4 x 4 matrices
- Hardware pipeline works with 4 dimensional representations
- For orthographic viewing, we can maintain w = 0 for vectors and w = 1 for points
- For perspective we need a perspective division

Change of Coordinate Systems (skip)

Consider two representations of the same vector with respect to two different basis (a[v₁, v₂, v₃] and b[u₁, u₂, u₃]). The representations are

Representing second basis in terms of first

Each of the basis vectors, u₁,u₂, u₃, are vectors that can be represented in terms of the first basis

The coefficients define a 3 x 3 matrix

and the basis can be related by

where a =[u₁, u₂, u₃]^T and b = [v₁, v₂, v₃]^T

see text for numerical examples

Change of Frames

We can apply a similar process in homogeneous coordinates to the representations of both points and vectors
Consider two frames

Any point or vector can be represented in each

Representing One Frame in Terms of the Other

Working with Representations

Within the two frames any point or vector has a representation of the same form
a=[a₁ a₂ a₃ a₄ ] in the first frame
b=[b₁ b₂ b₃ b₄ ] in the second frame
where a₄ = b₄ = 1 for points and a₄ = b₄ = 0 for vectors and

The matrix M is 4 x 4 and specifies an affine transformation in homogeneous coordinates

Affine Transformations

Every linear transformation is equivalent to a change in frames
Every affine transformation preserves lines
However, an affine transformation has only 12 degrees of freedom because 4 of the elements in the matrix are fixed and are a subset of all possible 4 x 4 linear transformations

The World and Camera Frames

When we work with representations, we work with n-tuples or arrays of scalars
Changes in frame are then defined by 4 x 4 matrices
In OpenGL, the base frame that we start with is the world frame
Eventually we represent entities in the camera frame by changing the world representation using the model-view matrix
Initially these frames are the same (M = I)

Moving the Camera

If objects are on both sides of z = 0, we must move the camera frame

This actually results in moving the world frame relative to the camera frame. To the programmer it appears that all points in front of the camera are now visible, by moving them down the z axis by -d units. This is almost always easier than attempting to change vertex coordinates to place the objects in a visible position.

See the text for a numerical example. In OpenGL this is easily accomplished by translating all points by [0, 0, -d] - more later, or by moving the camera to [0, 0, d] - more later, both produce the same result.