CHAPTER 8 - Implementation 2
- Introduce Mapping Methods
- Texture Mapping
- Environmental Mapping
- Bump Mapping
- Consider basic strategies
- Forward vs backward mapping
- Point sampling vs area averaging
The Limits of Geometric Modeling
- Although graphics cards can render over 10
million polygons per second, that number is insufficient for many
phenomena
- Clouds
- Grass
- Terrain
- Skin
Modeling an Orange
- Consider the problem of modeling an orange (the fruit)
- Start with an orange-colored sphere
- Too simple
- Replace sphere with a more complex shape
- Does not capture surface characteristics (small dimples)
- Takes too many polygons to model all the dimples
Modeling an Orange (2)
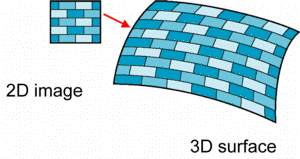
- Take a picture of a real orange, scan it,
and “paste” onto simple geometric model
- This process is known as texture mapping
- Still might not be sufficient because
resulting surface will be smooth
- Need to change local shape
- Bump mapping
Three Types of Mapping
- Texture Mapping
- Uses images to fill inside of polygons
- Environmental (reflection mapping)
- Uses a picture of the environment for texture maps
- Allows simulation of highly specular surfaces
- Bump mapping
- Emulates altering normal vectors during the rendering process
Texture Mapping

Environment Mapping

Bump Mapping

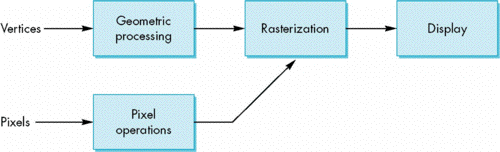
Where does mapping take place?
- Mapping techniques are implemented at the end of the rendering pipeline
- Very efficient because few polygons make it past the clipper
Is it simple?
- Although the idea is simple---map an image to a surface---there are 3 or 4 coordinate systems involved
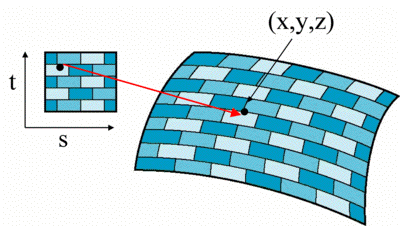
Coordinate Systems
- Parametric coordinates
- May be used to model curved surfaces
- Texture coordinates
- Used to identify points in the image to be mapped
- World Coordinates
- Conceptually, where the mapping takes place
- Screen Coordinates
- Where the final image is really produced
Texture Mapping

Mapping Functions
- Basic problem is how to find the maps
- Consider mapping from texture coordinates to a point on a surface
- Appear to need three functions
- x = x(s,t)
- y = y(s,t)
- z = z(s,t)
- But we really want to go the other way
Backward Mapping
- We really want to go backwards
- Given a pixel, we want to know to which point on an object it corresponds
- Given a point on an object, we want to know to which point in the texture it corresponds
- Need a map of the form
- s = s(x,y,z)
- t = t(x,y,z)
- Such functions are difficult to find in general
Two-part mapping
- One solution to the mapping problem is to first map the texture to a simple intermediate surface
- Example: map to cylinder

Cylindrical Mapping

Spherical Map
- We can use a parametric sphere
x = r cos 2
 u
uy = r sin 2
 u cos 2
u cos 2 v
vz = r sin 2
 u sin 2
u sin 2 v
v - in a similar manner to the cylinder but have to decide where to put the distortion
- Spheres are used in environmental maps
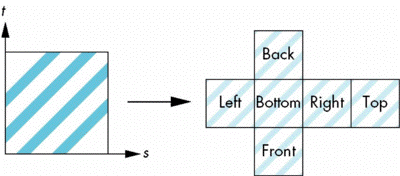
Box Mapping
- Easy to use with simple orthographic projection
- Also used in environmental maps
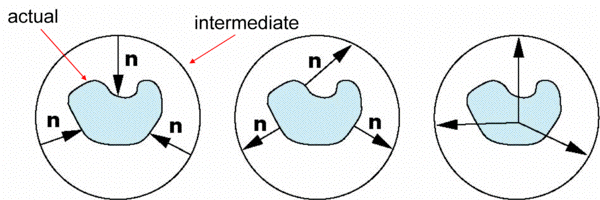
Second Mapping
- Map from intermediate object to actual
object
- Normals from intermediate to actual
- Normals from actual to intermediate
- Vectors from center of intermediate
Aliasing
- Point sampling of the texture can lead to aliasing errors
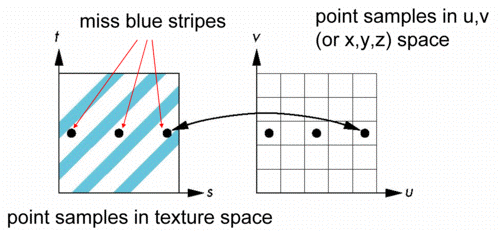
Area Averaging
- A better but slower option is to use area averaging
