chapter 4.4

Virtual Trackball

Objectives

Introduces the use of graphical (virtual) devices that can be created using OpenGL
Makes use of transformations
Leads to reusable code that will be helpful later

Physical Trackball

The trackball is an upside down mouse

If there is little friction between the ball and the rollers, we can give the ball a push and it will keep rolling yielding continuous changes
Two possible modes of operation
- Continuous pushing or tracking hand motion
- Spinning

A Trackball from a Mouse

Problem: we want to get the two behavior modes from a mouse
We would also like the mouse to emulate a frictionless (ideal) trackball
Solve in two steps
- Map trackball position to mouse position
- Use GLUT to obtain the proper modes

Trackball Frame

origin at center of ball

Projection of Trackball Position

We can relate position on trackball to position on a normalized mouse pad by projecting orthogonally onto pad

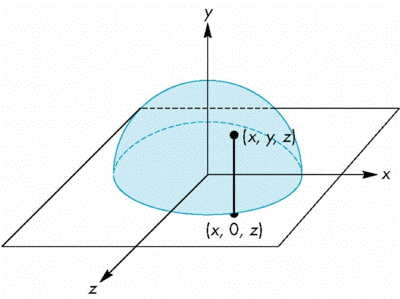
Reversing Projection

Because both the pad and the upper hemisphere of the ball are two-dimensional surfaces, we can reverse the projection
A point (x,z) on the mouse pad corresponds to the point (x,y,z) on the upper hemisphere where

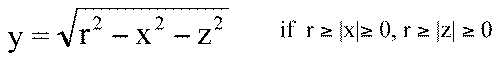
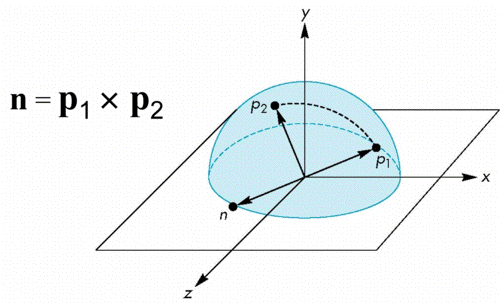
Computing Rotations

Suppose that we have two points that were obtained from the mouse.
We can project them up to the hemisphere to points p₁ and p₂
These points determine a great circle on the sphere
We can rotate from p₁ to p₂ by finding the proper axis of rotation and the angle between the points

Using the cross product

The axis of rotation is given by the normal to the plane determined by the origin, p1 , and p2

Obtaining the angle

The angle between p1 and p2 is given by

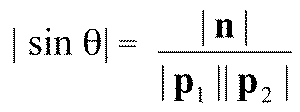
If we move the mouse slowly or sample its position frequently, then 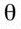will be small and we can use the approximation

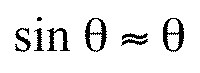
Implementing with GLUT

We will use the idle, motion, and mouse callbacks to implement the virtual trackball
Define actions in terms of three booleans
- trackingMouse: if true update trackball position
- redrawContinue: if true, idle function posts a redisplay
- trackballMove: if true, update rotation matrix

Example

In this example, we use the virtual trackball.c to rotate the color cube we modeled earlier
The code to examine is

//Initialization//The Projection Step //glutMotionFunc (1)//glutMotionFunc (2)//Idle and Display Callbacks//Mouse Callback//Start Function //Stop Function

Better Trackball code can be found in underwater.c in the mouse and motion callbacks.

Quaternions

Because the rotations are on the surface of a sphere, quaternions provide an interesting and more efficient way to implement the trackball
See code in some of the standard demos included with Mesa