CHAPTER 10 - Implementation 2

Objectives Objectives <next>

Build a tree-structured model of a humanoid figure
Examine various traversal strategies
Build a generalized tree-model structure that is independent of the particular model

Humanoid Figure

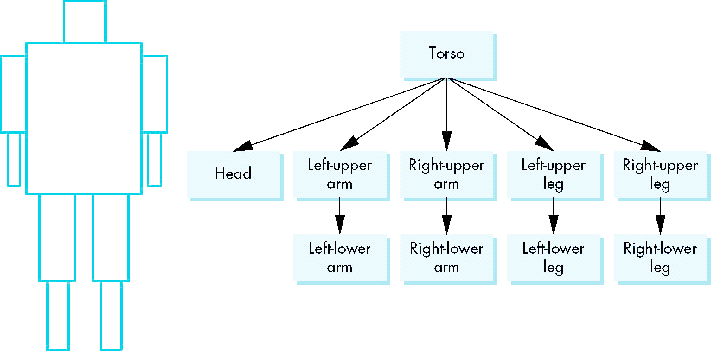
Building the Model

Can build a simple implementation using quadrics: ellipsoids and cylinders
Access parts through functions
- torso()
- left_upper_arm()
Matrices describe position of node with respect to its parent
- M_lla positions left lower leg with respect to left upper arm

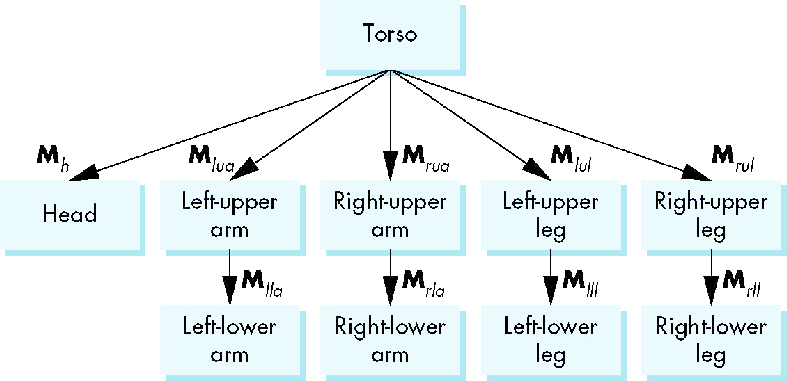
Tree with Matrices

Display and Traversal

The position of the figure is determined by 11 joint angles (two for the head and one for each other part)
Display of the tree requires a graph traversal
- Visit each node once
- Display function at each node that describes the part associated with the node, applying the correct transformation matrix for position and orientation

Transformation Matrices

There are 10 relevant matrices
- M positions and orients entire figure through the torso which is the root node
- M_h positions head with respect to torso
- M_lua, M_rua, M_lul, M_rul position arms and legs with respect to torso
- M_lla, M_rla, M_lll, M_rll position lower parts of limbs with respect to corresponding upper limbs

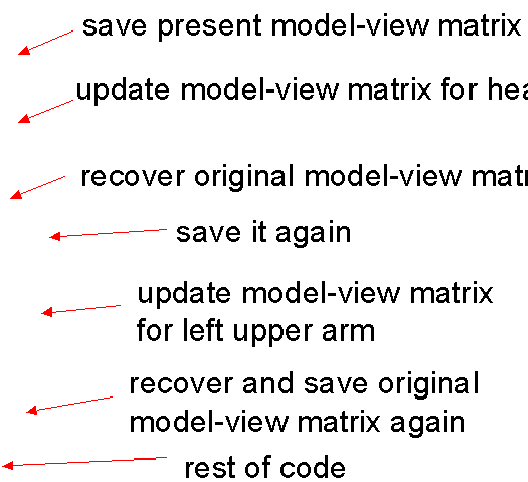
Stack-based Traversal

Set model-view matrix to M and draw torso
Set model-view matrix to MM_h and draw head
For left-upper arm need MM_lua and so on
Rather than recomputing MM_lua from scratch or using an inverse matrix, we can use the matrix stack to store M and other matrices as we traverse the tree

Traversal Code

Analysis

The code describes a particular tree and a particular traversal strategy
- Can we develop a more general approach?
Note that the sample code does not include state changes, such as changes to colors
- May also want to use glPushAttrib and glPopAttrib to protect against unexpected state changes affecting later parts of the code

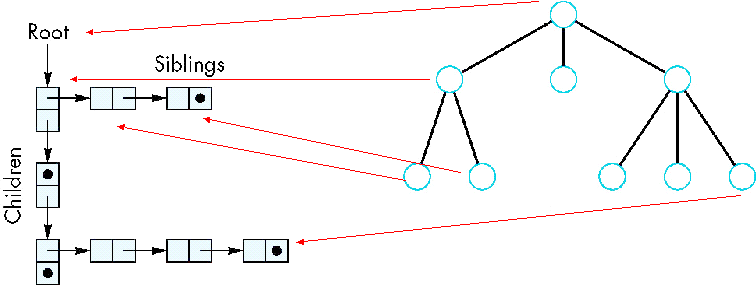
General Tree Data Structure

Need a data structure to represent tree and an algorithm to traverse the tree
We will use a left-child right sibling structure
- Uses linked lists
- Each node in data structure is two pointers
- Left: next node
- Right: linked list of children

Left-Child Right-Sibling Tree

Tree node Structure

At each node we need to store
- Pointer to sibling
- Pointer to child
- Pointer to a function that draws the object represented by the node
- Homogeneous coordinate matrix to multiply on the right of the current model-view matrix
  - Represents changes going from parent to node
  - In OpenGL this matrix is a 1D array storing matrix by columns

C Definition of treenode

typedef struct treenode {
Glfloat m[16];
void (*f)();
struct treenode *sibling;
struct treenode *child; } treenode;

Defining the torso node

treenode torso_node, head_node, lua_node, … ;
/* use OpenGL functions to form matrix */
glLoadIdentity();
glRotatef(theta[0], 0.0, 1.0, 0.0);
/* move model-view matrix to m */
glGetFloatv(GL_MODELVIEW_MATRIX, torso_node.m)
torso_node.f = torso; /* torso() draws torso */
Torso_node.sibling = NULL;
Torso_node.child = &head_node;

Notes

The position of figure is determined by 11 joint angles stored in theta[11]
Animate by changing the angles and redisplaying
We form the required matrices using glRotate and glTranslate
- More efficient than software
- Because the matrix is formed in model-view matrix, we may want to first push original model-view matrix on matrix stack

Preorder Traversal

void traverse(treenode *root) {

if(root == NULL) return;
glPushMatrix();
glMultMatrix(root->m);
root->f();
if(root->child != NULL) traverse(root->child);
glPopMatrix();
if(root->sibling != NULL) traverse(root->sibling);

Notes

We must save modelview matrix before multiplying it by node matrix
- Updated matrix applies to children of node but not to siblings which contain their own matrices
The traversal program applies to any left-child right-sibling tree
- The particular tree is encoded in the definition of the individual nodes
The order of traversal matters because of possible state changes in the functions

Dynamic Trees

If we use pointers, the structure can be dynamic
typedef treenode *tree_ptr; tree_ptr torso_ptr; torso_ptr = malloc(sizeof(treenode));
Definition of nodes and traversal are essentially the same as before but we can add and delete nodes during execution

<next>