CHAPTER 7 - Implementation 3

Objectives

Survey Line Drawing Algorithms
- DDA
- Bresenham

Rasterization

Rasterization (scan conversion)
- Shade pixels that are inside object specified by a set of vertices
  - Line segments
  - Polygons: scan conversion = fill
Shades determined by color, texture, shading model
Here we study algorithms for determining the correct pixels starting with the vertices

Scan Conversion of Line Segments

Start with line segment in window coordinates with integer values for endpoints
Assume implementation has a write_pixel function

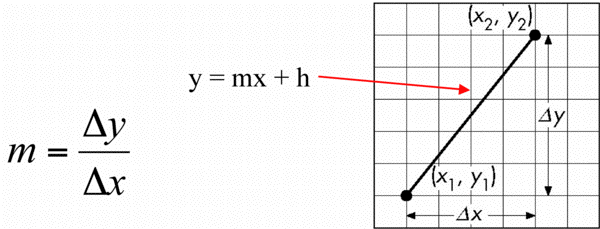
DDA Algorithm (Digital Differential Analyzer)

DDA was a mechanical device for numerical solution of differential equations

Line y = mx+ h satisfies differential equation
- dy/dx = m = 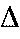y/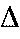x = (y2-y1)/(x2-x1)

Along scan line 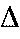x = 1

for(x = x1; x <= x2; x++) { y+=m; write_pixel(x, round(y), line_color) }

Problem

DDA = for each x plot pixel at closest y
- Problems for steep lines

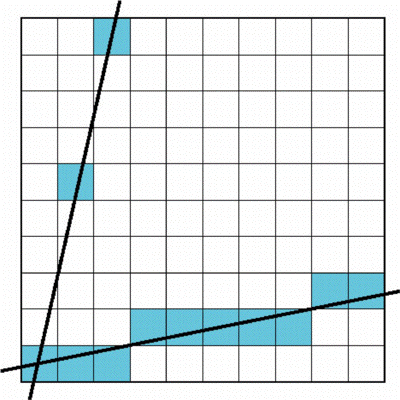
Using Symmetry

For m > 1, swap role of x and y
- For each y, plot closest x

Bresenham's Algorithm

DDA requires one floating point addition per step
We can eliminate all fp through Bresenham's algorithm
Consider only 0 <= m <= 1
- Other cases by symmetry
Assume pixel centers are at half integers
If we start at a pixel that has been written, there are only two candidates for the next pixel to be written into the frame buffer

Candidate Pixels

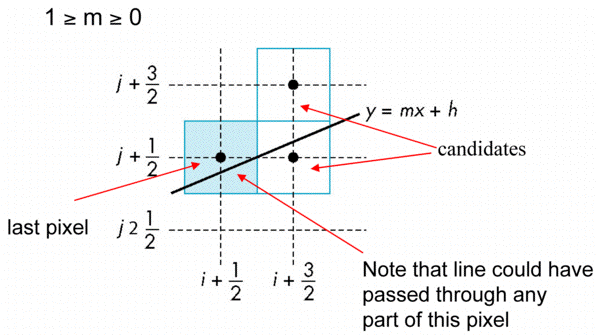
Decision Variable

Incremental Form

More efficient if we look at d_k, the value of the decision variable at x = k + 1/2

For each x, we need do only an integer addition and a test
Single instruction on graphics chips

Midpoint Line Algorithm (alternate discussion from Foley)

Bresenham [BRES65] developed this classic algorithm which uses integer arithmetic and thus removes the need for the round operation. It can also be applied to the integer computation of circles. The algorithm can be extended to handle lines with fp endpoints.

The algorithm assumes slopes are in [0,1] and the lower left endpoint is at (x0,y0) and the upper right endpoint is at (x1,y1).

Using the grid below for discussion.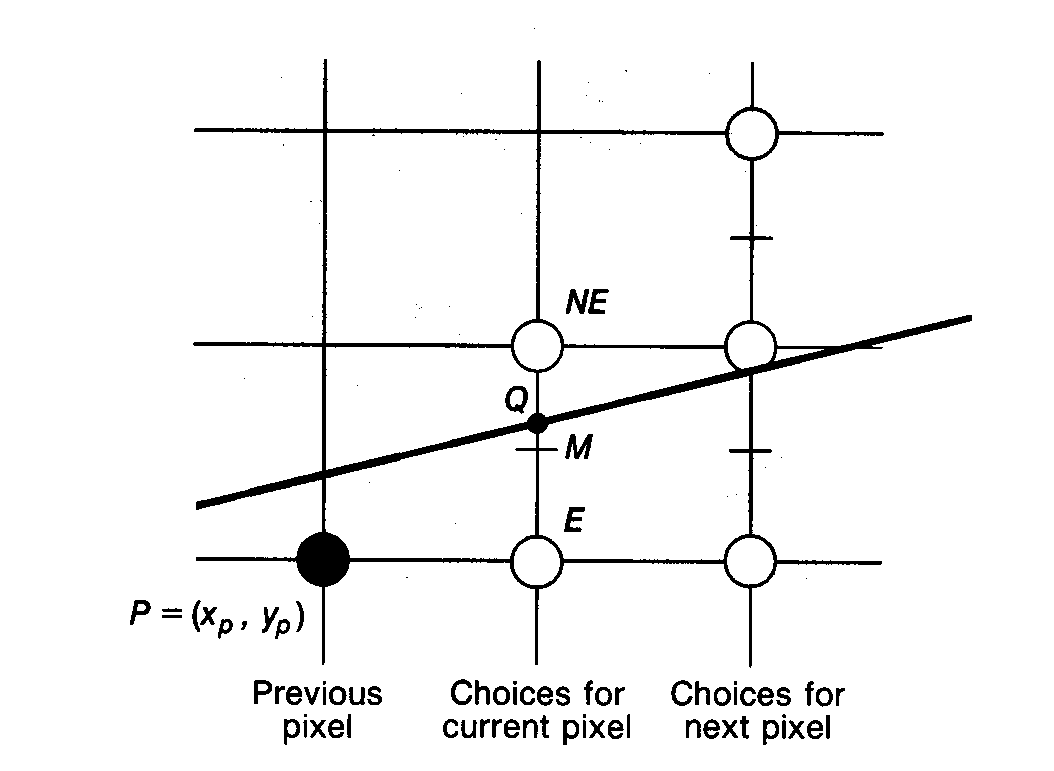

Assume pixel (xp,yp) has been selected to be displayed. Let point Q represent the intersection of the line we wish to draw with the line representing the vertical raster grid one pixel to the right of (xp,yp). We now have a choice, either select the pixel one increment to the right (pixel E) or select the pixel one increment to the right and one increment up (pixel NE).

Bresenham's algorithm computes the vertical distances from E to Q and from NE to Q. The sign of the difference is used to select the point whose distance from Q is smaller. This distance is always <= 1/2.

Algorithm :

Using the line function, (x,y) = ax + by + c = 0
and y = (dy/dx)x + B then (by subtr. y from both sides/mult. by dx)
F(x,y) = dy(x) - dx(y) + dx(B) = 0 where
a = dy, b = -dx, c = dx(B)
For points on the line F(x,y) = 0, F is positive for points below the line and negative for points above the line.

EXAMPLE

Consider the line defined by endpoints (1, 2) and (5, 3). Then dy = 3 - 2 = 1, dx = 5 - 1 = 4 and B is determined as y = (dy/dx)x + B or

2 = (1/4) 1 + B, where B = 7/4.

The point (2,1) is below the line and F(2,1) = (1) 2 - (4) 1 + (4)(7/4) = 5.

The point (2,4) is above the line and F(2,4) = (1) 2 - (4) 4 + (4) (7/4) = -7.

END EXAMPLE

To apply the midpoint criteria (assuming current point is (xp,yp)) we need to compute F(xp+1, yp+1/2) and test its sign. F at this point will be called the decision variable d = F(xp+1, yp+1/2).
By definition d = a(xp + 1) + b(yp + 1/2) + c.
if d > 0 then choose E point, if d < 0 then choose NE point, if d = 0 choose either, so pick E point.
Next we must determine the amount to increment which depends on the point chosen. If E is chosen then

dnew = F(xp+2,yp+1/2) = a(xp+2) + b(yp+1/2) + c

but

dold = a(xp+1) + b(yp+1/2) + c

If we subtract dold from dnew we get dnew = dold+a. Thus the /\E = a = dy

If NE is chosen then we increment in both directions and

dnew = F(xp+2,yp+3/2) = a(xp+2) + b(yp+3/2) + c

If we subtract dold from dnew we get dnew = dold+a+b. Thus the /\NE = a + b = dy - dx

To summarize: at each step choose between two pixels based on sign of decision variable d calculated in previous step. Update decision variable by /\E or /\NE depending on which point is chosen in current step.

To calculate the initial value of d to start the algorithm use the first endpoint (x0,y0) then

The first midpoint is at (x0+1, y0+1/2) and

F(x0+1,y0+1/2) = a(x0+1) +b(y0+1/2) + c

= ax0 + by0 + c + a + b/2

= F(x0,y0) + a + b/2 and since F(x0,y0) is a point on the line it = 0.
Thus dstart = a + b/2 = dy - dx/2
To get rid of the fraction redefine F(x,y) = 2(ax +by+c)which does not affect the sign of the decision variable which is all that is needed for the algorithm.

Polygon Scan Conversion

Scan Conversion = Fill
How to tell inside from outside
- Convex easy
- Nonsimple difficult
- Odd even test
  - Count edge crossings
- Winding number

Winding Number

Count clockwise encirclements of point

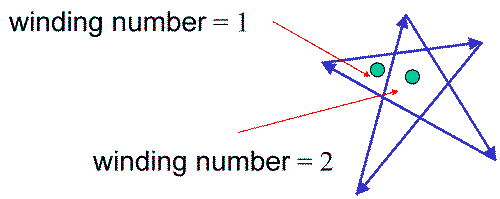
Alternate definition of inside: inside if winding number != 0

Filling in the Frame Buffer

Fill at end of pipeline
- Convex Polygons only
- Nonconvex polygons assumed to have been tessellated
- Shades (colors) have been computed for vertices (Gouraud shading)
- Combine with z-buffer algorithm
  - March across scan lines interpolating shades
  - Incremental work small

Using Interpolation

C1 C2 C3 specified by glColor or by vertex shading
C4 determined by interpolating between C1 and C2
C5 determined by interpolating between C2 and C3
- interpolate between C4 and C5 along span

Flood Fill

Fill can be done recursively if we know a seed point located inside (WHITE)
Scan convert edges into buffer in edge/inside color (BLACK)

flood_fill(int x, int y) {

if(read_pixel(x,y)= = WHITE) { write_pixel(x,y,BLACK); flood_fill(x-1, y); flood_fill(x+1, y); flood_fill(x, y+1); flood_fill(x, y-1); } }

Scan Line Fill

Can also fill by maintaining a data structure of all intersections of polygons with scan lines

Sort by scan line

Fill each span

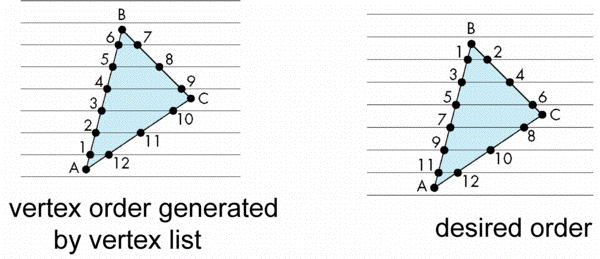
Data Structure

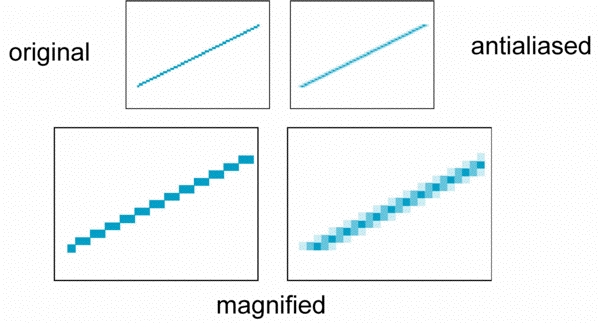
Aliasing

Ideal rasterized line should be 1 pixel wide

Choosing best y for each x (or visa versa) produces aliased raster lines

Antialiasing by Area Averaging

Color multiple pixels for each x depending on coverage by ideal line

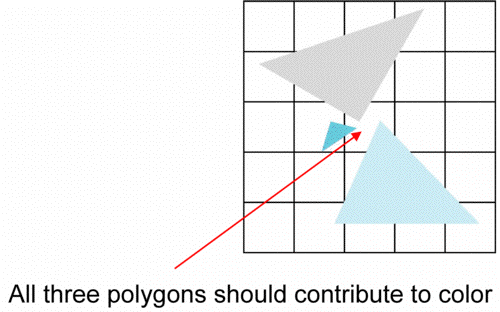
Polygon Aliasing

Aliasing problems can be serious for polygons

Jaggedness of edges

Small polygons neglected

Need compositing so color of one polygon does not totally determine color of pixel