chapter 5.2
- Introduce the mathematics of projection
- Introduce OpenGL viewing functions
- Look at alternate viewing APIs
Computer Viewing
- There are three aspects of the viewing process, all of which
are implemented in the pipeline,
- Positioning the camera
- Setting the model-view matrix
- Selecting a lens
- Setting the projection matrix
- Clipping
- Setting the view volume
- Positioning the camera
The OpenGL Camera
- In OpenGL, initially the world and camera frames are the
same
- Default model-view matrix is an identity
- The camera is located at origin and points in the negative z direction
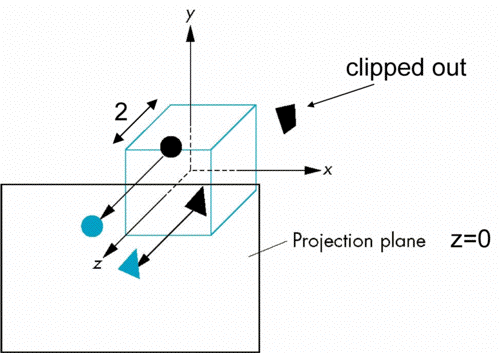
- OpenGL also specifies a default view volume that is a cube
with sides of length 2 centered at the origin
- Default projection matrix is an identity
Default Projection
- Default projection is orthogonal
Moving the Camera Frame
- If we want to visualize objects with both positive and
negative z values we can either
- Move the camera in the positive z direction
- Translate the camera frame
- Move the objects in the negative z direction
- Translate the world frame
- Move the camera in the positive z direction
- Both of these views are equivalent and are determined by the
model-view matrix
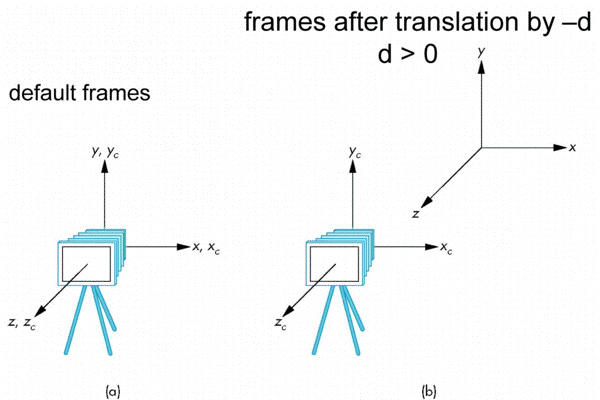
- Want a translation (glTranslatef(0.0,0.0,-d);)
- d > 0
Moving Camera back from Origin
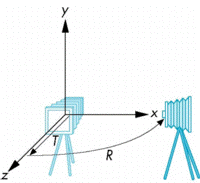
Moving the Camera
- We can move the camera to any desired position by a sequence of rotations and translations
- Example: side view
- Rotate the camera
- Move it away from origin
- Model-view matrix C = TR
OpenGL code
- Remember that last transformation specified is first to be
applied
glMatrixMode(GL_MODELVIEW)
glLoadIdentity();
glTranslatef(0.0, 0.0, -d);
glRotatef(90.0, 0.0, 1.0, 0.0);
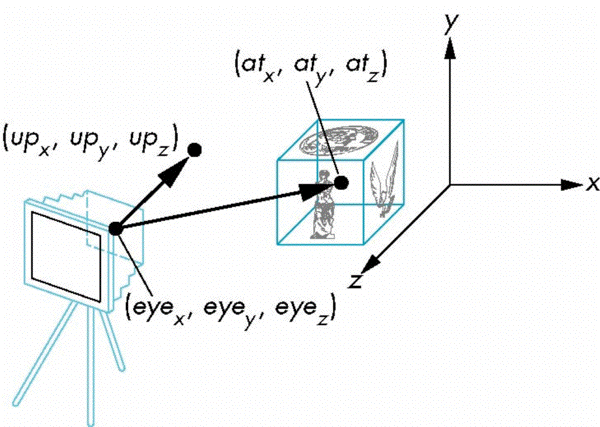
The LookAt Function
- The GLU library contains the function gluLookAt to form the required modelview matrix through a simple interface
- Note the need for setting an up direction
- Still need to initialize
- Can concatenate with modeling transformations
- Example: isometric view of cube aligned with axes cubeview2.c
based on (cubeview.c , cube.c)
glMatrixMode(GL_MODELVIEW):
glLoadIdentity();
gluLookAt(1.0, 1.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0. 0.0);
gluLookAt
glLookAt(eyex, eyey, eyez, atx, aty, atz, upx, upy, upz)
Other Viewing APIs
- The LookAt function is only one possible API for positioning the camera
- Others include
- View reference point, view plane normal, view up (PHIGS, GKS-3D)
- Yaw, pitch, roll
- Elevation, azimuth, twist
- Direction angles
Projections and Normalization - (Read Section 5.4 carefully)
- The default projection in the eye (camera) frame is orthogonal
- For points within the default view volume
xp = x
yp = y
zp = 0 - Most graphics systems use view normalization (canonical form of view volume)
- All other views are converted to the default view by transformations that determine the projection matrix
- Allows use of the same pipeline for all views
Homogeneous Coordinate Representation

Simple Perspective
- Center of projection at the origin
- Projection plane z = d, d < 0

Perspective Equations
- Consider top and side views

Homogeneous Coordinate Form (Error in
image; substitute p = Mq in statement consider q = Mp where)

Perspective Division
- However w != 1, so we must divide by w to return from homogeneous coordinates
- This perspective division yields the desired perspective equations

- We will consider the corresponding clipping volume with the OpenGL functions
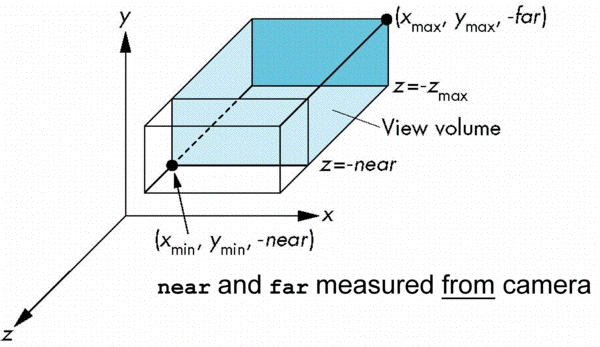
OpenGL Orthogonal Viewing
glOrtho(xmin,xmax,ymin,ymax,near,far)
glOrtho(left,right,bottom,top,near,far)
OpenGL Perspective
glFrustum(xmin,xmax,ymin,ymax,near,far)

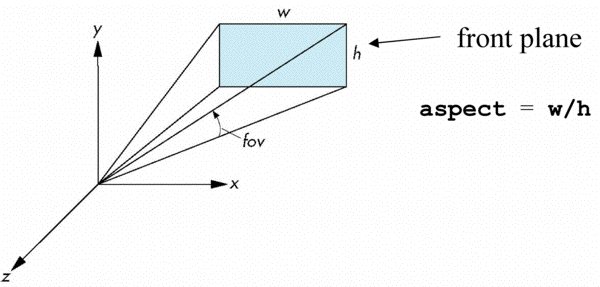
Using Field of View
- With glFrustum it is often difficult to get the desired view
gluPerpective(fovy, aspect, near, far)often provides a better interface