PDAs and CFGs

Solutions 1: a, b, c, d. 2: a, b, c, d. 3: h, i, j;

---

Solutions

NPDAs
Construct non-deterministic pushdown automata to accept the following languages.
a. {1ⁿ0ⁿ | n>0}

 

 

 

 

b. {0ⁿ1²ⁿ | n>=0}

 

 

 

 

 

c. {1ⁿ0ⁿ | n>0} U {0ⁿ1²ⁿ | n>=0}

 

 

 

 

 

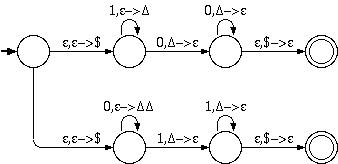
d. (0+1)* - {ww | w in {0,1}*} (complement of ww)

 

 

 

 

 

 

DPDAs
Construct deterministic pushdown automata to accept the following languages.
a. {10ⁿ1ⁿ | n>0} U {110ⁿ1²ⁿ | n>0}

 

 

 

 

 

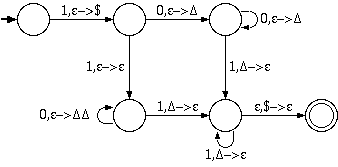
b. Binary strings that contain an equal number of 1s and 0s.

 

 

 

 

 

c. Binary strings with twice as many 1s as 0s.

 

 

 

 

 

 

d. Binary strings that start and end with the same symbol and have the same number of 0s as 1s.

 

 

 

 

 

 

 

 

 

 

CFGs
Construct context free grammars to accept the following languages.
e. (2.4b) {w | w starts and ends with the same symbol}

f. (2.4c) {w | |w| is odd}

g. (2.4d) {w | |w| is odd and its middle symbol is 0}

 

 

 

 

h. {0ⁿ1ⁿ | n>0} U {0ⁿ1²ⁿ | n>0}

S -> 0A1 | 0B11
A -> 0A1 | e
B -> 0B11 | e

 

 

 

 

 

i. {0ⁱ1^j2^k | i!=j or j!=k}

S -> AC | BC | DE | DF
A -> 0 | 0A | 0A1
B -> 1 | B1 | 0B1
C -> 2 | 2C
D -> 0 | 0D
E -> 1 | 1E | 1E2
F -> 2 | F2 | 1F2

 

 

 

 

 

j. Binary strings with twice as many 1s as 0s.

S -> e | 0S1S1S | 1S0S1S | 1S1S0S