Terrain maps
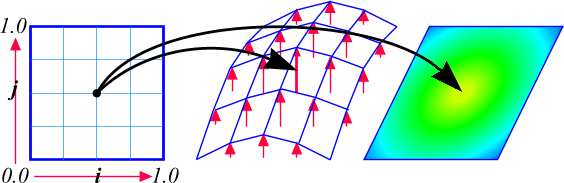
A terrain map is a function that maps a 2D coordinate (x,y)
to an altitude a and color c. In
other words, a
terrain map is simply a function that describes the
topography of a
small area.
|
A terrain map
|
Terrain as an interface:
public interface Terrain {
public double getAltitude (double i,
double j);
public RGB getColor (double i, double j);
}
Assume
that 0.0 <= i, j,altitude <= 1.0. This
is not a
requirement, but will give a good idea where to find
the terrain being
viewed. The color of the
terrain is
described simply as an RGB triplet. The following
class will do:
public class RGB {
private double r, g, b;
public RGB (double r, double g, double b)
{
this.r = r;
this.g = g;
this.b = b;
}
public RGB add (RGB rgb) {
return new RGB (r + rgb.r, g +
rgb.g, b +
rgb.b);
}
public RGB subtract (RGB rgb) {
return new RGB (r - rgb.r, g -
rgb.g, b -
rgb.b);
}
public RGB scale (double scale) {
return new RGB (r * scale, g *
scale, b *
scale);
}
private int toInt (double value) {
return (value < 0.0) ? 0 :
(value > 1.0)
? 255 :
(int) (value *
255.0);
}
public int toRGB () {
return (0xff << 24) |
(toInt (r) <<
16) |
(toInt (g)
<< 8) | toInt (b);
}
}
The RGB class defines a
simple color container. Some basic facilities for
performing color
arithmetic and converting a floating-point color to
packed-integer
format are provided.
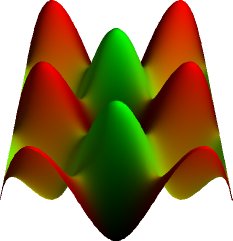
Transcendental
terrains
Start by looking at a transcendental terrain --
a terrain computed from sines and cosines:
|
A transcendental terrain map
|
public class TranscendentalTerrain implements Terrain
{
private double alpha, beta;
public TranscendentalTerrain (double
alpha, double beta) {
this.alpha = alpha;
this.beta = beta;
}
public double getAltitude (double i,
double j) {
return .5 + .5 * Math.sin (i *
alpha) *
Math.cos (j * beta);
}
public RGB getColor (double i, double j) {
return new RGB (.5 + .5 *
Math.sin (i *
alpha),.5 - .5 * Math.cos (j * beta), 0.0);
}
}
The constructor accepts two values
that
define the frequency of the terrain. These are used to
compute
altitudes and colors using Math.sin()
and Math.cos().
These functions return values -1.0 <= sin(),
cos() <= 1.0,
so the return values are adjusted accordingly.
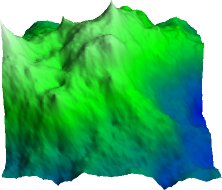
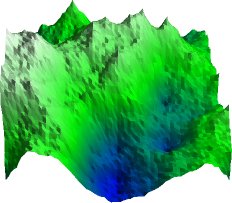
Fractal Terrains
Simple mathematical terrains are no fun. What we want is something that looks at least passably real. We could use real topography files as our terrain map (the San Francisco Bay or the surface of Mars, for example). What we really want is something that looks passably real and has never been seen before.
|
A fractal terrain map
|
A fractal is something (a function or object) that exhibits self-similarity. For example, the Mandelbrot set is a fractal function: if you magnify the Mandelbrot set greatly you will find tiny internal structures that resemble the main Mandelbrot itself. A mountain range is also fractal, at least in appearance. From close up, small features of an individual mountain resemble large features of the mountain range, even down to the roughness of individual boulders. This principal of self-similarity is used to generate fractal terrains.
Essentially a coarse, initial random terrain is generated. Then additional random details are recursively added that mimic the structure of the whole, but on increasingly smaller scales. The actual algorithm that is used, the Diamond-Square algorithm, was originally described by Fournier, Fussell, and Carpenter in 1982 (see Resources for details).
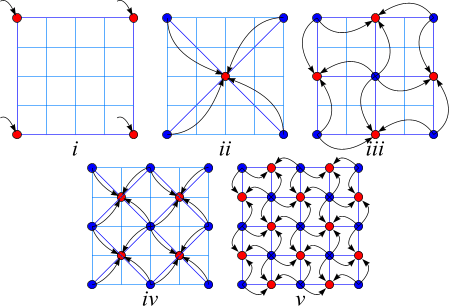
These are the steps to build the fractal terrain:
- Assign a random height to the four corner points of
a
grid.
- Take the average of these four corners, add a
random
perturbation and assign this to the midpoint of the
grid (ii
in the following diagram). This is called the diamond
step
because we are creating a diamond pattern on the grid.
(At the first
iteration the diamonds don't look like diamonds
because they are at the
edge of the grid; but if you look at the diagram
you'll understand the
concept.)
- Take each of the diamonds produced, average the
four
corners, add a random perturbation and assign this to
the diamond
midpoint (iii in the following diagram). This
is called the square
step because we are creating a square pattern on the
grid.
- Next, reapply the diamond step to each square created in the square step, then reapply the square step to each diamond created in the diamond step, and so on until the grid is sufficiently dense.
|
The Diamond-Square algorithm
|
An obvious question arises: How much to perturb the grid? The answer is to start with a roughness coefficient 0.0 < roughness < 1.0. At iteration n of the Diamond-Square algorithm add a random perturbation to the grid: -roughnessn <= perturbation <= roughnessn. Essentially, as finer detail is added to the grid, the scale of changes is reduced. Small changes at a small scale are fractally similar to large changes at a larger scale.
If a small value is used for roughness, then the terrain will be very smooth -- the changes will very rapidly diminish to zero. If a large value is chosen, then the terrain will be very rough, as the changes remain significant at small grid divisions.
|
A rough (.6) fractal terrain
|
Here's the code to implement the fractal terrain map:
public
class FractalTerrain implements Terrain {
private double[][] terrain;
private double roughness, min, max;
private int divisions;
private Random rng;
public FractalTerrain (int lod, double
roughness) {
this.roughness = roughness;
this.divisions = 1 <<
lod;
terrain = new double[divisions
+ 1][divisions +
1];
rng = new Random ();
terrain[0][0] = rnd ();
terrain[0][divisions] = rnd
();
terrain[divisions][divisions]
= rnd ();
terrain[divisions][0] = rnd
();
double rough =
roughness;
for (int i = 0; i < lod; ++
i) {
int r = 1
<< (lod - i), s = r >> 1;
for (int j = 0; j
< divisions; j
+= r)
for
(int k = 0; k <
divisions; k += r)
diamond
(j,
k, r, rough);
if (s > 0)
for
(int j = 0; j <=
divisions; j += s)
for
(int k
= (j + s) % r; k <= divisions; k += r)
square
(j
- s, k - s, r, rough);
rough *=
roughness;
}
min = max = terrain[0][0];
for (int i = 0; i <=
divisions; ++ i)
for (int j = 0; j
<= divisions;
++ j)
if
(terrain[i][j] <
min) min = terrain[i][j];
else
if (terrain[i][j]
> max) max = terrain[i][j];
}
private void diamond (int x, int y, int
side, double scale)
{
if (side > 1) {
int half = side /
2;
double avg =
(terrain[x][y] +
terrain[x + side][y] +
terrain[x
+ side][y +
side] + terrain[x][y + side]) * 0.25;
terrain[x +
half][y + half] = avg +
rnd () * scale;
}
}
private
void square (int x, int y, int side, double scale) {
int half = side / 2;
double avg = 0.0, sum = 0.0;
if (x >= 0)
{ avg += terrain[x][y + half];
sum += 1.0; }
if (y >= 0)
{ avg += terrain[x + half][y];
sum += 1.0; }
if (x + side <= divisions)
{ avg += terrain[x + side][y +
half]; sum +=
1.0; }
if (y + side <= divisions)
{ avg += terrain[x + half][y +
side]; sum +=
1.0; }
terrain[x + half][y + half] =
avg / sum + rnd
() * scale;
}
private double rnd () {
return 2. * rng.nextDouble ()
- 1.0;
}
public double getAltitude (double i,
double j) {
double alt = terrain[(int) (i
*
divisions)][(int) (j * divisions)];
return (alt - min) / (max -
min);
}
private
RGB blue = new RGB (0.0, 0.0, 1.0);
private RGB green = new RGB (0.0, 1.0,
0.0);
private RGB white = new RGB (1.0, 1.0,
1.0);
public RGB getColor (double i, double j) {
double a = getAltitude (i, j);
if (a < .5)
return blue.add
(green.subtract
(blue).scale ((a - 0.0) / 0.5));
else
return green.add
(white.subtract
(green).scale ((a - 0.5) / 0.5));
}
}
In the constructor, specify both the roughness
coefficient roughness and the level of
detail lod.
The level of detail is the number of iterations to
perform -- for a
level of detail n, a grid of (2n+1
x 2n+1)
samples is produced. For each iteration, apply the
diamond step to each
square in the grid and then the square step to each
diamond.
Afterwards, compute the minimum and maximum sample
values, which are
used to scale the terrain altitudes.
To compute the altitude of a point, scale and return the closest grid sample to the requested location. Ideally, interpolation between surrounding sample points gives the best results, but this method is simpler, and good enough at this point. In the final application this issue will not arise because we will actually match the locations where we sample the terrain to the level of detail that we request. To color the terrain, simply return a value between blue, green, and white, depending upon the altitude of the sample point.
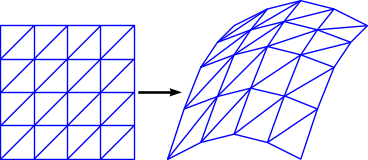
Tessellating the terrain
A terrain map is now defined over a square domain. It is
necessary
to decide how to actually draw this onto the screen. The
following
describes how to approximate the smooth terrain with a
bunch of
connected triangles -- that is, a tessellation of the
terrain.
Tessellate: to form into or adorn with mosaic (from the Latin tessellatus).
To form the triangle mesh, evenly sample the terrain into a regular grid and then cover this grid with triangles -- two for each square of the grid.
The following code fragment populates the elements of the terrain grid with fractal terrain data. The vertical axis of the terrain is scaled to make the altitudes a bit less exaggerated.
double exaggeration = .7;
int lod = 5;
int steps = 1 << lod;
Triple[] map = new Triple[steps + 1][steps + 1];
Triple[] colors = new RGB[steps + 1][steps + 1];
Terrain terrain = new FractalTerrain (lod, .5);
for (int i = 0; i <= steps; ++ i) {
for (int j = 0; j <= steps; ++ j) {
double x = 1.0 * i /
steps, z = 1.0 * j / steps;
double altitude =
terrain.getAltitude (x, z);
map[i][j] = new Triple (x,
altitude *
exaggeration,
z);
colors[i][j] =
terrain.getColor (x, z);
}
}
|
Tessellating the terrain
|
So why triangles and not squares? The problem with using the squares of the grid is that they're not flat in 3D space. If you consider four random points in space, it's extremely unlikely that they'll be coplanar. So instead, decomposing the terrain to triangles guarantees that any three points in space will be coplanar. This means that there'll be no gaps in the terrain.
public
class Triangle {
private int[] i = new int[3];
private int[] j = new int[3];
private Triple n;
private RGB[] rgb = new RGB[3];
private Color color;
public Triangle (int i0, int j0, int i1,
int j1, int i2,
int j2) {
i[0] = i0;
i[1] = i1;
i[2] = i2;
j[0] = j0;
j[1] = j1;
j[2] = j2;
}
}
The Triangle data structure stores each
vertex as an index (i,j) into the gridpoints
of our terrain,
along with normal and color information that is filled
in later. Create
the array of triangles with the following piece of code:
int numTriangles = (steps * steps * 2);
Triangle[] triangles = new Triangle[numTriangles];
int triangle = 0;
for (int i = 0; i < steps; ++ i) {
for (int j = 0; j < steps; ++ j) {
triangles[triangle ++] = new
Triangle (i, j, i
+ 1, j, i, j + 1);
triangles[triangle ++] = new
Triangle (i + 1,
j, i + 1, j + 1, i, j + 1);
}
}
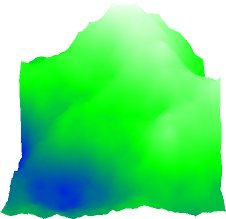
Lighting and shadows
The colored terrain is not much to boast about. Without
performing some lighting and shadow computation the
terrain looks like
this:
|
A terrain without lighting
|
The first improvement will add ambient and diffuse light sources so that elements of the landscape are lit according to their orientation relative to the sun. Next shadows are added.
Lighting
In a nutshell, if a diffuse (matte) surface is facing a light source, the amount of reflected light will be proportional to the cosine of the angle of incidence of the light on the surface. Light falling directly on a surface will be strongly reflected; light falling at an oblique angle will be weakly reflected. In addition, all surfaces will be evenly lit by an amount of ambient, directionless light.
|
A diffusely lit terrain
|
This simple lighting model is applied to the terrain. One option is to take each point on the terrain and compute whether the point is facing the sun, and if so, what the angle of incidence is; the cosine of the angle of incidence is equal to the dot product of the terrain normal and sunlight direction. Of course, doing this for every point in the scene is rather expensive. Instead, perform this calculation once for every triangle.
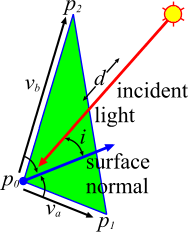
First, compute a vector from the sun to the terrain:
sun: psun = (xsun, ysun, zsun) terrain point: p = (x, y, z) light vector: vlight = p - psun = (x - xsun, y - ysun, z - zsun)
To aid in these computations, use a helper class:
public
class Triple {
private double x, y, z;
public Triple (double x, double y, double
z) {
this.x = x;
this.y = y;
this.z = z;
}
public Triple add (Triple t) {
return new Triple (x + t.x, y
+ t.y, z + t.z);
}
public Triple subtract (Triple t) {
return new Triple (x - t.x, y
- t.y, z - t.z);
}
public Triple cross (Triple t) {
return new Triple (y * t.z - z
* t.y, z * t.x -
x * t.z,
x * t.y - y *
t.x);
}
public
double dot (Triple t) {
return x * t.x + y * t.y + z *
t.z;
}
public double length2 () {
return dot (this);
}
public Triple normalize () {
return scale (1.0 / Math.sqrt
(length2 ()));
}
public Triple scale (double scale) {
return new Triple (x * scale,
y * scale, z *
scale);
}
}
The Triple class represents a point or
vector in space, and provides methods that allow various
mathematical
operations to be performed.
Next, the surface normal is computed. Take two (non-parallel) vectors in the plane of the triangle and compute their cross product to produce the surface normal. And, to select two vectors in the plane of the triangle, just take two sides of the triangle:
-
Triangle: T = [p0, p1,
p2]
Sides: va = (p1 - p0) = (x1 - x0, y1 - y0, z1 - z0); vb = (p2 - p0) = (x2 - x0, y2 - y0, z2 - z0)
Surface normal: nT = va x vb = (yazb - zayb, zaxb - xazb, xayb - yaxb)
Next, remember that the strength of the light drops off in proportion to the inverse square of its distance from its source. This makes sense if you remember that the surface area of a sphere is 4.pi.r2, so at a distance from the sun d, the light emitted from the sun will be spread over an area of 4.pi.d2. For us on earth, it doesn't really matter; the strength of light from the sun is about one one hundredth of a percent weaker on the far side of the earth than the near. For our scene, however, the sun will be very close, so we care about this computation.
|
Computing the diffuse surface lighting
|
Now compute the illumination of a point on the terrain using the surface normal, the light direction, and the distance from the sun. The diffuse lighting is proportional to the cosine of the angle of the light's incidence, which is the dot product of two unit vectors. The ambient lighting is a constant. So...
-
Ambient lighting: a
Sun's strength: s
Unit surface normal: n' = n / |n|
Light distance: d = |vlight|
Unit light vector: v'light = v / d
Light incidence: i = v'light . n'
Illumination facing the sun: (i < 0) : l = a - i . s / d2
Illumination facing away from the sun: (i >= 0) : l = a
That's it. We can now compute the amount of light reflected by any triangle in our terrain map.
Shading
An immediate fault apparent in the above image is that
the
triangles are flat shaded: each triangle has
but a single
color. This goes somewhat against the grain of a terrain
definition --
terrains are D0 continuous in
altitude and color,
but we then render each triangle in a single color. This
means that the
image is not D0 continuous.
Adjacent triangles
have different colors, and the image shouldn't have any
absolute color
discontinuities.
To overcome this dilemma use Gouraud shading to compute a color for each vertex of each triangle and then smoothly interpolate between these vertex colors within the triangle.
|
A Gouraud-shaded triangle
|
The Gouraud shading model easily ensures D0 continuity. Simply compute a color at each grid point on the terrain, and then assign the triangle vertices the appropriate colors from the grid. If two triangles are adjacent, they will share the same vertices along their common edge, and so will share exactly the same color along that edge.
|
A terrain with Gouraud shading
|
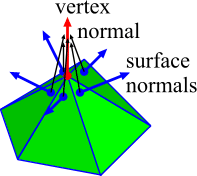
To determine the color at a point on our grid, use the exact computations outlined earlier. The only additional information needed is the surface normal at the terrain vertices. This can be computed in a couple of ways. Given that triangle surface normals are computed anyway, one easy option is to simply average the surface normals of all triangles sharing the vertex.
|
Computing vertex normals
|
The following code computes the normals and lighting information for the array of triangles:
double
ambient = .3;
double diffuse = 4.0;
Triple[][] normals = new Triple[steps + 1][steps + 1];
Triple sun = new Triple (3.6, 3.9, 0.6);
for (int i = 0; i < numTriangles; ++ i)
for (int j = 0; j < 3; ++ j)
normals[i][j] = new Triple
(0.0, 0.0, 0.0);
/* compute triangle normals and vertex averaged
normals */
for (int i = 0; i < numTriangles; ++ i) {
Triple v0 =
map[triangles[i].i[0]][triangles[i].j[0]],
v1 =
map[triangles[i].i[1]][triangles[i].j[1]],
v2 =
map[triangles[i].i[2]][triangles[i].j[2]];
Triple normal = v0.subtract (v1).cross
(v2.subtract
(v1)).normalize ();
triangles[i].n = normal;
for (int j = 0; j < 3; ++ j) {
normals[triangles[i].i[j]][triangles[i].j[j]]
=
normals[triangles[i].i[j]][triangles[i].j[j]].add
(normal);
}
}
/*
compute vertex colors and triangle average colors */
for (int i = 0; i < numTriangles; ++ i) {
RGB avg = new RGB (0.0, 0.0, 0.0);
for (int j = 0; j < 3; ++ j) {
int k = triangles[i].i[j], l =
triangles[i].j[j];
Triple vertex = map[k][l];
RGB color = colors[k][l];
Triple normal =
normals[k][l].normalize ();
Triple light = vertex.subtract
(sun);
double distance2 =
light.length2 ();
double dot = light.normalize
().dot (normal);
double lighting = ambient +
diffuse * ((dot
< 0.0) ? - dot : 0.0) / distance2;
color = color.scale
(lighting);
triangles[i].color[j] = color;
avg = avg.add (color);
}
triangles[i].color = new Color (avg.scale
(1.0 / 3.0).toRGB
());
}
One obvious fault with this implementation is there are no sharp edges, even where there are meant to be sharp edges. For example, along the edge of a shadow there should be a sharp discontinuity. In the above implementation, however, triangles on both sides of the shadow will blur the edge. This is even worse along a sharp color discontinuity in the terrain -- for example, where the blue sea meets the yellow sand. Solving this problem is simply a matter of adding more information to the model, and not sharing certain vertex colors. That is not covered in this project.
Shadows
Almost all of the static precomputations needed to
generate
the terrain data structure are complete. One last thing
to notice is
that when a given part of the terrain is facing the sun
or not, we
don't check to see if the terrain element is shadowed by
another part
of the terrain.
Doing a fully accurate shadow computation would involve projecting the entire terrain back down onto itself, as seen from the sun, and then subdividing triangles into shaded and unshaded parts.
|
Computing accurate shadows
|
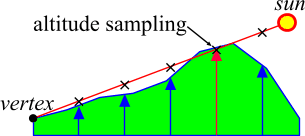
This process, however, is slow and difficult. Instead, we'll go with a stopgap measure that gives some degree of realism at greatly reduced complexity. For every point on the terrain grid trace a line from the terrain to the sun, and determine whether this line intersects the terrain at any other point. If it does, the point is in shadow; if it does not, compute lighting as usual.
|
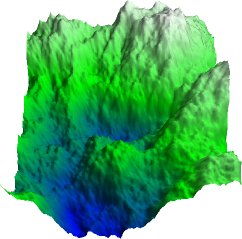
A terrain with shadows
|
Furthermore, in order to make this computation more efficient, we won't perform a proper terrain intersection test. Instead, simply sample the line at various points along its length, and check whether the terrain altitude at these points is higher than the line.
|
Computing simple shadows
|
The following code performs these shadow calculations. Use the computed shadow array in a slightly modified version of the earlier shadow computation: if a vertex is in shadow then there is no diffuse lighting; only ambient.
double[][]
shade = new double[steps + 1][steps + 1];
for (int i = 0; i <= steps; ++ i) {
for (int j = 0; j <= steps; ++ j) {
shade[i][j] = 1.0;
Triple vertex = map[i][j];
Triple ray = sun.subtract
(vertex);
double distance = steps *
Math.sqrt (ray.x *
ray.x + ray.z * ray.z);
/* step along ray in
horizontal units of grid
width */
for (double place = 1.0; place
< distance;
place += 1.0; {
Triple sample =
vertex.add
(ray.scale (place / distance));
double sx =
sample.x, sy =
sample.y, sz = sample.z;
if ((sx < 0.0)
|| (sx > 1.0)
|| (sz < 0.0) || (sz > 1.0))
break;
/* steppd off
terrain */
double ground =
exaggeration *
terrain.getAltitude (sx, sz);
if (ground >=
sy) {
shade[i][j]
= 0.0;
break;
}
}
}
}
/*
modified lighting computation:
...
double shadow = shade[k][l];
double lighting = ambient +
diffuse * ((dot
< 0.0) ? - dot : 0.0) /
distance2
*
shadow;
*/
This solution is not perfect. If
there
is a sharp ridge or peak in the terrain, some vertices
in the shadow of
the feature realize that they are in shadow, and others
do not. The
typical problem is that the line sampling for some
vertices falls on
the feature (we get shadow), and for others it just
skips over the
feature (we get light). To overcome this problem, a
proper intersection
test is needed. Practically speaking, just sample the
shadow line more
frequently. The above solution steps along the shadow
line in jumps the
size of the terrain grid. If you find shadow artifacts,
reduce the
step.
-
Resources
- JavaSoft's Java 3D API: A comprehensive graphics
library
http://java.sun.com/products/java-media/3D/
- UCB CS184: Using Quaternions to Represent Rotation
http://www.cs.berkeley.edu/~laura/cs184/quat/quaternion.html
- Stop by Michael Garnland's terrain simplification
page,
which includes sample terrains
http://www.cs.cmu.edu/~garland/scape/
- Read Ken Musgrave's "Building Fractal Planets"
http://www.seas.gwu.edu/faculty/musgrave/article.html
Read "Computer Rendering of Stochastic Models" by Alain Fournier, Don Fussell, and Loren Carpenter (Communications of the ACM, Jun 1982, p.371) - Download the complete source for this article as a
gzipped
tar file
http://www.javaworld.com/jw-08-1998/step/jw-08-step.tar.gz
- Download the complete source for this article as a zip
file
http://www.javaworld.com/jw-08-1998/step/jw-08-step.zip
- Read all the previous Step by Step
articles from Shoffner and Hughes
http://www.javaworld.com/topicalindex/jw-ti-step.html