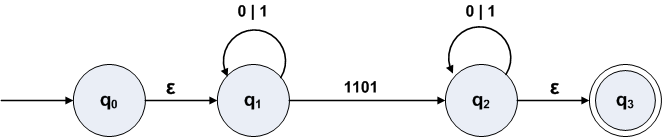
A GNFA for strings in {1,0} that contain the substring "1101".
A Generalized Nondeterministic Finite Automaton is similar to an NFA but the transition function takes a state and a regular expression in the alphabet instead of a state and an alphabet element.

A GNFA for strings in {1,0} that contain the substring "1101".
The idea is that in state q0 the
transition to state q1 can be taken if the next input matches
the regular expression 1101.
The formal definition is given (on page 73) by:
A generalized nondeterministic finite automaton is a 5-tuple, (Q,∑, δ, qstart, qaccept), where
Note that there is only one accept state. However, this is no real restriction for a nondetrministic automaton. (Why?)
On the other hand, the transition function is defined on a different arguments than is the case for an ordinary NFA.
The transition function, δ, for the example GNFA:

is
| q1 | q2 | q3 | |
|---|---|---|---|
| q0 | ε | ⌀ | ⌀ |
| q1 | (0 | 1) | 1101 | ⌀ |
| q2 | ⌀ | (0 | 1) | ε |
The definition of the language of a GNFA is technically different than that of an NFA because the transition function is defined differently. However, the idea is really similar, but extended to allow regular expressions on the transitions.
The formal definition is given by (page 73):
A GNFA accepts a string w in ∑* if w =
w1w2...wk, where each wi
is in ∑* and a sequence of states q0, q1,
..., qk exists such that
The string 0011011 is accepted by

If 0011011 is partitioned into blocks w1=ε w2=0 w3=0 w4=1101 w5=1 w6=ε; that is,
0011011 = ε 0 0 1101 1 ε
then
| State | Input | Next | |
| w1=ε ∊ L(δ(q0, q1)) | q0 | w1 | q1 |
| w2=0 ∊ L(δ(q1, q1)) | q1 | w2 | q1 |
| w3=0 ∊ L(δ(q1, q1)) | q1 | w3 | q1 |
| w4=1101 ∊ L(δ(q1, q2)) | q1 | w4 | q2 |
| w5=1 ∊ L(δ(q2, q2)) | q2 | w5 | q2 |
| w6=ε ∊ L(δ(q2, q3)) | q2 | w6 | q3 |
For example, w1=ε ∊ L(δ(q0, q1)) means for state q0 and input w1, next state is q1
An NFA can be converted to an equivalent GNFA by
δ'(qi, qj) = a if and only if δ(qi, a) = qj
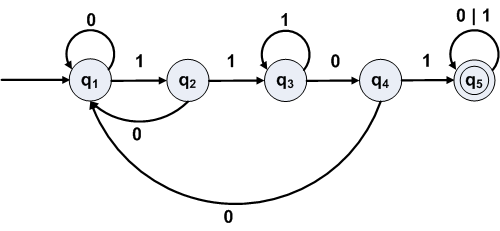
Steps 1 and 2 require adding a new start state and a new accepting state. Step 3 require no changes in the diagram except labeling the transitions out of the new start state and into the new accepting state.
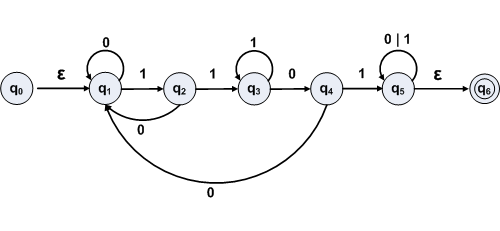
Any state except the start state and the accept state of a GNFA can be eliminated to obtain a new equivalent GNFA with one fewer states.
For example, to eliminate state q1 in

There are 3 arrows coming into state q1 from other states: q0, q2, and q4.
If state q1 is removed, paths must be replaced by new transitions:

Eliminating q1, what regular expressions are needed?
Suppose qa is to be removed and
Then the path from qi to qj should be labeled
RiaRaa*Raj ∪ Rij
Original NFA (converted to a GNFA):

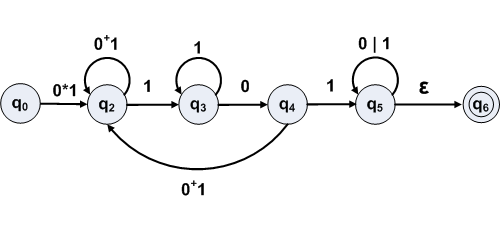
After eliminating state q1, recalculate labels for paths that went through q1:
| Path | Label Expression |
Actual Label |
|---|---|---|
| q0 to q2 | R01R11*R12 ∪ R02 | ε0*1 ∪ empty = 0*1 |
| q2 to q2 | R21R11*R12 ∪ R22 | 00*1 ∪ empty = 0+1 |
| q4 to q2 | R41R11*R12 ∪ R42 | 00*1 ∪ empty = 0+1 |
To show the first part, if we are given an NFA, we need to show that there is a regular expression that describes exactly the language of the NFA.
The construction of the regular expression begins with the NFA and each step will eliminate one state of the NFA until the only state(s) remaining are the start state and a final state.
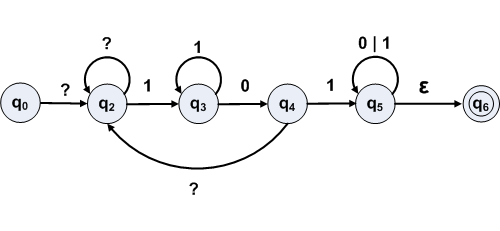
Exercise 1.16a
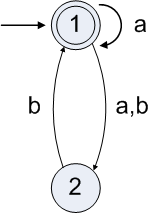
Convert this NFA to a regular expression that describes the same language.
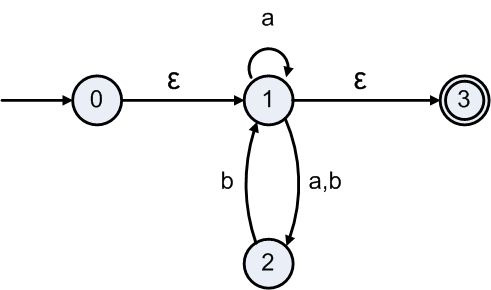
Eliminate non-start, non-final state 1.
Recalculate labels for paths through state 1
| Path | Label Expression |
Actual Label |
|---|---|---|
| 0 to 3 | R01R11*R13 ∪ R03 | εa*ε ∪ empty = a* |
| 0 to 2 | R01R11*R12 ∪ R02 | εa*(a|b) ∪ empty = a*(a|b) |
| 2 to 3 | R21R11*R13 ∪ R23 | ba*ε ∪ empty = ba* |
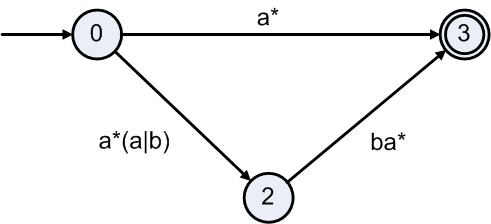

Finally eliminate state 2. Only one path remains from 0 to 3. Recalculate the label for the path through state 2.
| Path | Label Expression |
Actual Label |
|---|---|---|
| 0 to 3 | R02R22*R23 ∪ R03 | a*(a|b)ε*ba* ∪ a* = a*(a|b)ba* | a* |

A regular expression that describes the same language as this NFA is
a*(a|b)ba* | a*
To show that for any regular expression there is an NFA that recognizes the same language described by the regular expression, the proof describes a procedure for constructing the NFA from the regular expression.
See Lemma 1.55 in the text.
Example regular expression
a(ba)*b ∪ bab