Data Structures and Algorithms
Searching Revisited

Before we examine some more searching techniques, we need to consider some operations on trees - in particular means of traversing trees.

Tree operations

A binary tree can be traversed in a number of ways:
pre-order
  1. Visit the root
  2. Traverse the left sub-tree,
  3. Traverse the right sub-tree
in-order
  1. Traverse the left sub-tree,
  2. Visit the root
  3. Traverse the right sub-tree
post-order
  1. Traverse the left sub-tree,
  2. Traverse the right sub-tree
  3. Visit the root

If we traverse the standard ordered binary tree in-order, then we will visit all the nodes in sorted order.

Parse trees

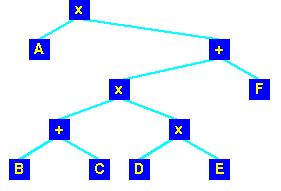
If we represent the expression:

A*(((B+C)*(D*E))+F)

as a tree:

then traversing it post-order will produce:
A B C + D E * * F + *
which is the familiar reverse-polish notation used by a compiler for evaluating the expression.

Search Trees

We've seen how to use a heap to maintain a balanced tree for a priority queue. What about a tree used to store information for retrieval (but not removal)? We want to be able to find any item quickly in such a tree based on the value of its key. The search routine on a binary tree: 
tree_search(tree T, Key key) {
    if (T == NULL) return NULL;
    if (key == T->root) return T->root;
    else
        if (key < T->root) return tree_search( T->left, key );
        else               return tree_search( T->right, key );
    }
is simple and provides us with a O(log n) searching routine as long as we can keep the tree balanced. However, if we simply add items to a tree, producing an unbalanced tree is easy!
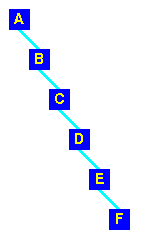
This is what happens if
we add the letters

A B C D E F

in that order to a tree:

Not exactly well balanced!

Key terms

Pre-order tree traversal
Traversing a tree in the order: root | left | right
In-order tree traversal
Traversing a tree in the order: left | root | right
Post-order tree traversal
Traversing a tree in the order: left | right | root