Algorithms: Trees

Algorithms

Trees

Binary Trees The simplest form of tree is a binary tree. A binary tree consists of

a node (called the root node) and
left and right sub-trees.
Both the sub-trees are themselves binary trees.

You now have a recursively defined data structure.

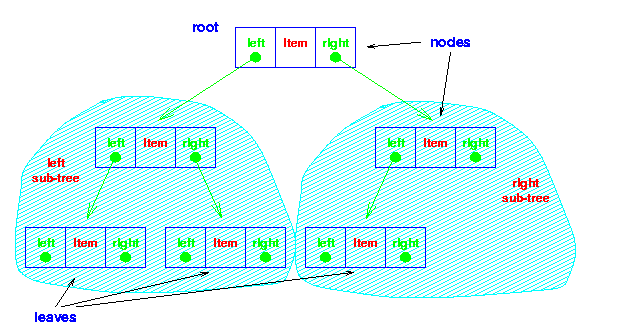
A binary tree

The nodes at the lowest levels of the tree (the ones with no sub-trees) are called leaves.

In an ordered binary tree,

the keys of all the nodes in the left sub-tree are less than that of the root,
the keys of all the nodes in the right sub-tree are greater than that of the root,
the left and right sub-trees are themselves ordered binary trees.

Data Structure

The data structure for the tree implementation simply adds left and right pointers in place of the next pointer of the linked list implementation.

Analysis

Complete Trees

Before we look at more general cases, let's make the optimistic assumption that we've managed to fill our tree neatly, ie that each leaf is the same 'distance' from the root.

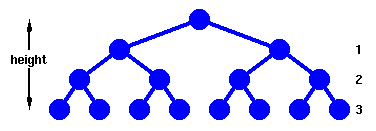
A complete tree

This forms a complete tree, whose height is defined as the number of links from the root to the deepest leaf.

First, we need to work out how many nodes, n, we have in such a tree of height, h.

Now,

n = 1 + 2¹ + 2² + .... + 2^h

From which we have,

n = 2^h+1 - 1

and

h = floor( log₂n )

Examination of the TreeSearch method shows that in the worst case, h+1 or ceiling( log₂n ) comparisons are needed to find an item. This is the same as for binary search.

However, TreeInsertion also requires ceiling( log₂n ) comparisons to determine where to add an item. Actually adding the item takes a constant number of operations, so we say that a binary tree requires O(logn) operations for both adding and finding an item - a considerable improvement over binary search for a dynamic structure which often requires addition of new items.

Deletion is also an O(logn) operation.

General binary trees

However, in general addition of items to an ordered tree will not produce a complete tree. The worst case occurs if we add an ordered list of items to a tree.

What will happen? Think before you click here!

This problem is readily overcome: we use a structure known as a heap.

Key terms

Root Node: Node at the "top" of a tree - the one from which all operations on the tree commence. The root node may not exist (a NULL tree with no nodes in it) or have 0, 1 or 2 children in a binary tree.
Leaf Node: Node at the "bottom" of a tree - farthest from the root. Leaf nodes have no children.
Complete Tree: Tree in which each leaf is at the same distance from the root. A more precise and formal definition of a complete tree is set out later.
Height: Number of nodes which must be traversed from the root to reach a leaf of a tree.