An AVL tree is another balanced
binary search tree. Named after their inventors, Adelson-Velskii
and Landis, they were the first dynamically balanced trees
to be proposed. Like red-black trees, they are not perfectly
balanced, but pairs of sub-trees differ in height by at most 1,
maintaining an O(logn) search time. Addition
and deletion operations also take O(logn)
time.
Definition of an AVL tree
An AVL tree is a binary search
tree which has the following properties:
- The sub-trees of every node differ in height by at
most one.
- Every sub-tree is an AVL tree.
|
 |
| |
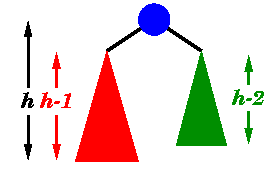
Balance requirement for an AVL tree: the left and
right sub-trees differ by at most 1 in height. |
You need to be careful with this definition: it permits some
apparently unbalanced trees! For example, here are some trees:
| Tree |
AVL tree? |
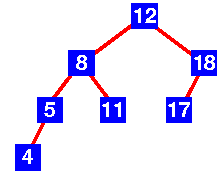 |
Yes
Examination shows that each left sub-tree has a
height 1 greater than each right sub-tree. |
 |
No
Sub-tree with root 8 has height 4 and sub-tree with root
18 has height 2 |
Insertion
As with the red-black tree, insertion is somewhat complex and
involves a number of cases. Implementations of AVL tree insertion
may be found in many textbooks: they rely on adding an extra
attribute, the balance
factor to each node. This factor indicates
whether the tree is left-heavy (the height of the left
sub-tree is 1 greater than the right sub-tree), balanced
(both sub-trees are the same height) or right-heavy (the
height of the right sub-tree is 1 greater than the left sub-tree).
If the balance would be destroyed by an insertion, a rotation is
performed to correct the balance.
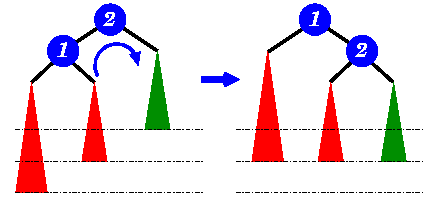 |
A new item has been added to the left subtree of node 1,
causing its height to become 2 greater than 2's right
sub-tree (shown in green). A right-rotation is performed to
correct the imbalance. |
- AVL trees
- Trees which remain balanced - and thus guarantee O(logn)
search times - in a dynamic environment. Or more importantly,
since any tree can be re-balanced - but at considerable cost -
can be re-balanced in O(logn) time.




